A lot of people have wondered why there's so much concern about COVID-19. I've taught classes on both differential equations and graph theory before with some degree of disease modeling, so I have some relevant expertise, although certainly much less than a trained epidemiologist or someone whose research focuses on disease modeling. In that context, I want to discuss some of the reasons why this is generating more concern than the regular flu from a mathematical standpoint.
The most common basic model of disease spread is the SIR model , and it turns out that simple versions of this model work pretty well empirically for many diseases. The basic idea of the model is that one has three compartments representing three types of people, people who are susceptible to the disease but are uninfected, people who are infected, and people who have recovered. People move from the susceptible to the infected category based on the number of people infected, with some parameter representing how likely an infected person is to infect new people. People move from the infected to the recovered population at some fixed probability. Strictly speaking "recovered" for our purposes also includes people who died and thus aren't spreading the disease but that distinction doesn't matter much for this sort of model. The basic model assumes that once one is in the recovered category one is either dead or immune.
When one uses this sort of model, and one looks at the disease presence over time the basic pattern one gets is a large hump followed by the number of infected then trailing downwards. For a graph of this sort of hump occurring in China with this virus, along with a lot of other good data, see here.
This is the basic model, and one can do a lot of things to play with the model. For example, one can imagine one has a vaccine for some people; this moves some people directly from the susceptible box into the recovered box. This drastically reduces the size of one's hump. Another thing one can do is have more than three boxes; one can imagine each region (say a city, school or nation) with its own set of boxes but then a chance for people infected in a region to infect people in a nearby region. One can also imagine diseases which have long periods of spread and infection, so the presence of births in the population become relevant. A good exercise is to think of some other thing you'd want to add to this sort of model.
As these models get more complicated, much of the modeling becomes empirical, running many different small variants of a model with computer approximations rather than much emphasis on analytic techniques; there's not as much as we can satisfactorily prove about some of these models as we'd like from a mathematician's perspective.
In this context, let's talk about three things which make from an SIR perspective this virus to be potentially worse than influenza (aside from the higher mortality rate which while also concerning isn't something that the SIR perspective really models much):
First, not everyone who gets the virus becomes immune after they recover; we're seeing not just relapses but evidence of reinfection. One essentially has some people who would move from infected to recovered but instead are moving back to susceptible. If one plays around with SIR models one will see that having such movement can easily make epidemics much worse. We're not completely certain that such reinfection is occurring but it looks likely. One difficulty is trying to distinguish reinfection from relapse. There's some evidence for low-level infections in people who are otherwise considered to have recovered. Trying to figure this out is going to be something doctors are thinking about very carefully. This is a general news article discussing some of the issues involved.
Second, the contagion rate of this virus appears to be higher than that for influenza. While there's a lot of uncertainty about the reproduction rate, R_0, which roughly speaking, represents the number of average new infections from infected individual, those numbers range from about 2.2 to about 4.5 and they seem to be likely on the higher end. In contrasts, many estimates for influenza put this number for it at at most 2; for the 1918 flu the number was probably between 2 and 3. Increasing R_0 has for what should be obvious reasons, a pretty severe impact on the severity of epidemics. The exact translation of R_0 into the SIR has some subtleties, and estimates for R_0 do change for diseases. They frequently start off larger than they would be otherwise until procedures targeting a disease are in place. There's some substantial criticism of R_0 as a metric in general , but as a rough guide it is useful here. There's also been some statement by the WHO (such as here) saying that at least by some metrics, COVID-19 is less efficient at transmission than the flu. I''m not sure what metrics they are using there, but if that's accurate that's a major reason to be less worried.
Third, there are people who get infected and are contagious but are almost completely asymptomatic. That basically doesn't happen with flu almost at all, and that means that containment is much harder. (This is not double counting evidence with the R_0 point above because those estimates are generally for people who do exhibit symptoms.) We're still uncertain how often this happens. In the case of influenza, people can be infectious before any substantial symptoms appear, but symptoms always show up. In the case of this virus, there appear to be some people, especially young people, who are not just infectious while being asymptomatic, but remain completely asymptomatic. Even a tiny percentage here can drastically interfere with containment efforts. Remember how I mentioned how one variant of SIR models involves triplets of boxes each for a different location? Well, if you do that, you can model how effective travel restrictions and quarantines are, and they become substantially less helpful if there are completely asymptomatic people. It only takes one infected person to enter a new location.
Right now one of the biggest issues is simply how many unknowns there are. It could turn out that all three of these issues above aren't that severe. Or it could turn out that all three are substantially in play. We don't completely know at this point, and have a worrying amount of evidence that all three of these issues are cropping up.
Right now one of the biggest issues is simply how many unknowns there are. It could turn out that all three of these issues above aren't that severe. Or it could turn out that all three are substantially in play. We don't completely know at this point, and have a worrying amount of evidence that all three of these issues are cropping up.
In this context, one might wonder why taking steps to delay infection matter. In these models, people get infected and eventually move over to recovered, so you might think that everyone gets infected. But that's not actually the case. Eventually, a disease becomes low enough levels that some people who are in the susceptible box category never get infected. If one can delay infection the number of people left in that box at the end stages can get bigger. Another major issue is the maximum number of infected. Remember the hump I mentioned above? The size of that hump matters a lot from a treatment perspective because ill people aren't as economically productive and many of them will need to be in hospitals, taking up limited hospital bed space. Even if the total number of infected were to remain the same over the entire period, the stress on the hospital system will be lower, resulting in likely fewer deaths from the disease, or deaths from other medical issues as the entire system is subject to less of a resource crunch. There's also the issue that other treatments may be developed; the longer we delay things the higher the chances that more people will be saved by new treatments. 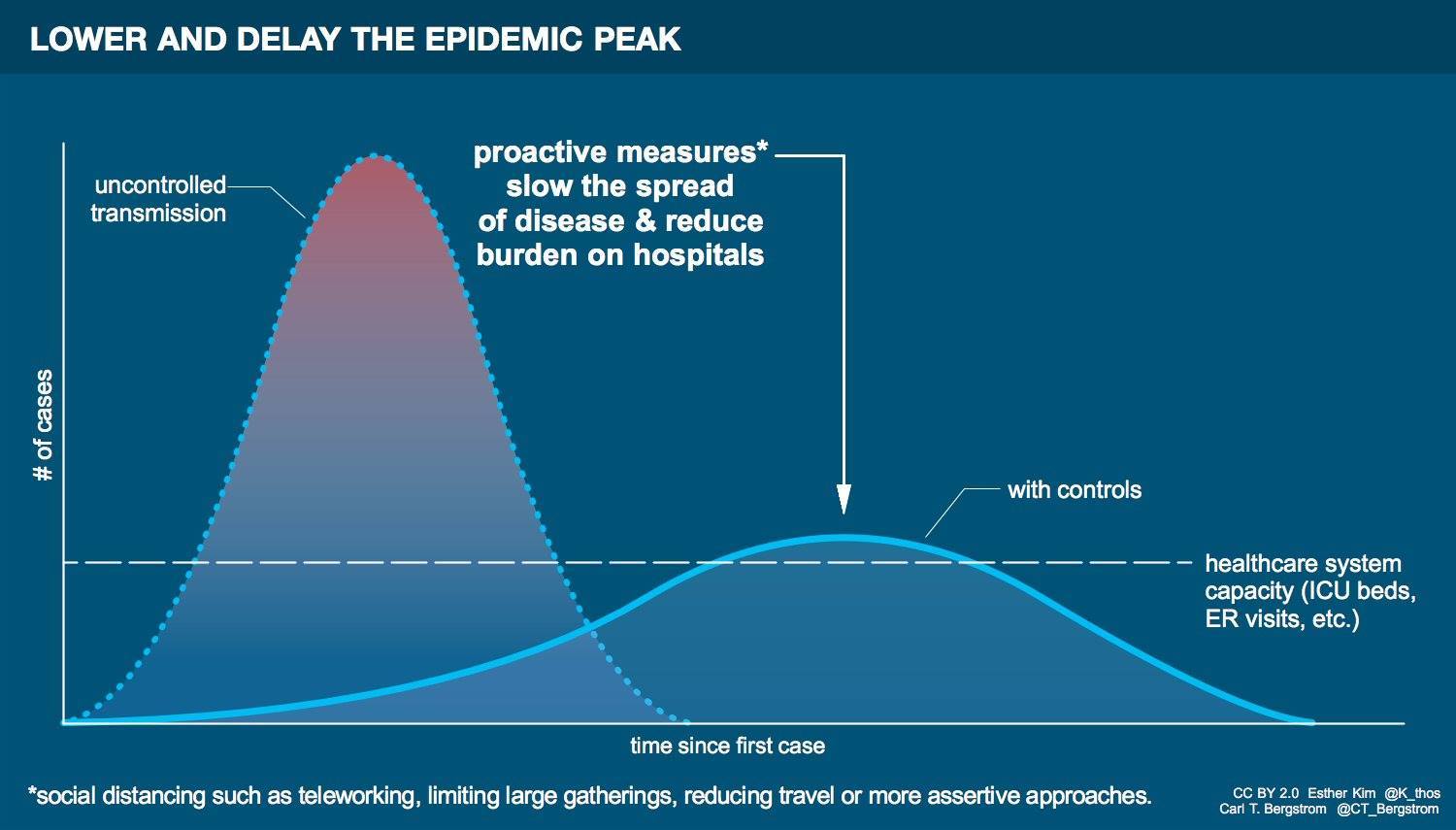

In this context, what can you do? Washing hands and not shaking hands are steps which have been mentioned by many but I'll repeat them here; they can't be emphasized enough. But aside from that, buying extra non-perishable goods that are frequently used is the obvious place to start. One doesn't need at this point to run out and buy all the toilet paper (looking at you Australia), but having a few extra days of food, and yes toiletries, is not a bad step. When you go to the store, buy a few extra food items. You don't need to buy them all now, but but buy a few, and then put them away, and (this bit is a important) don't count them as present when calculating whether you need to pick up more food in the future, until the disease is passed. The same goes for some other basic items, medicines and the like when possible and practical.
Another thingy you can do is get the flu vaccine. While Trump's comments about the flu vaccine for COVID-19 were, not surprisingly, stupid and ignorant, there are two good reasons to get the flu vaccine if you have not before. First, for many diseases, multiple infections are a major cause of fatalities. With the 1918 flu, many who died died not directly from influenza but from bacterial infections which occurred with it and this is a pretty standard pattern for deaths from influenza or similar illnesses. Second, the flu vaccine makes it less likely that one will need to be hospitalized for flu; that's even more important now than it usually is, because of the possible issues with limited hospital resources. If we can minimize stressing the system as a whole, we'll be in better shape.