Diophantine Equations

(Note: I'm in the process of copying some older math posts from Facebook over here. This is the first of those.)

 

 In school, one often learns to solve equations in a single variable, something like x^2-5x+6=0. But when one has more than one variable what can one say about the solution set? For example, one might have x^2 -2y^2 =1 which has a lot of solutions. 

One thing we're interested in is equations with possibly more than one variable, but we only care about integer solutions. For example, in our equation x^2- 2y^2 =1, we might care about solutions like x=1, y=0, or x=-1 and y=0, or the solution x=3 and y=2, but we won't care about solutions like x=2 and y = 1.225 ... When we care about an equation's integer solutions only we'll call it a Diophatine equation. This is a term named after the Greek mathematician who studied similar equations; most of the time Diophantus himself was interested in the slightly broader set of rational solutions, but the name stuck. It turns out that x^2 -2y^2 =1 has infinitely many integer solutions, but establishing that takes more work.

 

Sometimes a Diophantine equation has no solutions at all. For example, let's look at x^2 + y^2 = 3. How can we tell that this equation has no integer solutions? Well, one way of doing so is to notice that if x=a and y=b is a solution, then so is x=-a, and y=-b, because x and y are always squared in this equation, and (-m)^2 = m^2 for any m. But, if x is at least 2, then x^2 is at least 4, and 4+0 is already greater than 3, so we need only look at options where x and y are either 0 or 1. Now, we can just check the possibilities 1^2+0=1 which is not 3, and 0^2+0^2 = 0 which is not 3, and 1^2+1^2 = 2 which is not 3.

 

What about a slightly harder equation? What if we want to look at the Diophantine equation x^2 + y^2 = 3+4t. It seems like this equation should be much harder than the previous one. Any proof that this equation doesn't have any solutions should trickier than the proof that x^2+y^2 = 3, because that equation is a special case of this one; in particular that equation is when we insist that t=0 in our new equation.

 

It seems that our previous method won't work because if t is big, then x or y could be large also. So for x^2+y^2=3+4t we can't in any obvious way reduce the set of solutions to just a finite set to check. Or can we?

 

Instead of looking at a finite set of integers, we'll look at the remainders of x and y when we divide by 4. We'll write the remainder of a when divided by b as "a (mod b)", and we'll say that two numbers are equivalent mod b if they have the same remainder when we divide by b. For example, 10, 4 and 16 are all equivalent mod 6, because they all leave a remainder of 4 when we divide by 6. Similarly, 5 and 9 are not equivalent mod 3, because 5 leaves a remainder of 2 when we divide by 3, but 9 leaves a remainder of 0. Let's look at the remainders of n^2 when we divide by 4.

1^2 = 1 = 1 (mod 4) . 2^2 = 4= 0 (mod 4), 3^2 = 9 = 1 (mod 4), 4^2 = 16 = 0 (mod 4). We might notice a pattern here, that any perfect square leaves a remainder of either 1 or 0 when we divide by 4.

 

Let's see why that's the case. If n is an even number then we can write n=2k for some integer k. Then n^2 = (2k)^2 = 4k^2 = 4(k^2) so n^2 leaves a remainder of 0 when we divide by 4. If n is odd, then n=2k+1 for some k, and in that case n^2 = (2k+1)^2 = 4k^2+4k+1 = 4(k^2 +k)+1 so, n^2 in that case leaves a remainder of 1 when we divide by 4.

 

Great, how is this relevant to trying to understand whether x^2 + y^2 = 3+4t has any integer solutions? Here's the key: we know that x^2 has a remainder of 1 or 0 when we divide by 4, and the same goes for y^2, so their sum x^2 + y^2 can have a remainder of 1+0, 0+1, 1+1 or 0+0 when we divide by 4. That means that no matter what values we choose for x and y, x^2 + y^2 will have a remainder of 0, 1 or 2 when we divide by 4; it will never have a remainder of 3. But 3+4t will always have a remainder of 3 when we divide by 4. So, there's no way that two sides can ever be equal, because their remainders will always be different.

 

One can often use this sort of approach. For example, one can look at remainders when dividing by 3, to show that x^2 = 2 + 3y doesn't have any integer solutions. (This is a good exercise.)

 

Sometimes an equation has no solutions other than a "trivial" solution. For example, we could take our earlier equation x^2 + y^2 = 3+4t and modify it to get (x^2 + y^2)(x^2 + y^2 + t^2) = (3+4t)(x^2 + y^2 + t^2). This new equation has a silly solution, x = y=t=0. But it doesn't have any other solutions; to see this note that if x^2 + y^2 + t^2 is not zero, then we can divide by it so we get just our original equation x^2 + y^2 = 3+4t back. But if x^2+y^2+t^2 =0, then we must have x=y=t=0.

 

Many equations have a solution where all the variables are zero, but no other solutions. For example, x^2 = 2y^2 only has the solution x=0 and y=0 (See if you can see why.)

 

One might hope that maybe when a Diophantine equation doesn't have solutions other than a trivial solution, one can always use these methods, either just looking at remainders, or being able to bound how big the variables can be and solving accordingly, or at least other similarly simple methods. But alas, this is not the case. There are equations where there are no solutions, but where no remainder argument will ever show you that.

A somewhat "famous" example is the Cassels-Guy cubic 5x^3 + 9y^3 + 10z^3 + 12w^3 = 0

This Diophantine equation has no solutions other than all variables being equal zero, but if you pick any n and try to look at the remainders when one divides by n, you'll never get a contradiction just from that, and in a certain deeper sense, even techniques which generalize the remainder argument won't ever tell you that there are no solutions. And if one lists other similarly simple methods, one can show that they won't lead to a contradiction either.

 

The Cassels-Guy cubic is annoying for another related reason. One might naively guess that if an equation has lots of variables that it should have non-zero solutions as long as there aren't any such remainder issues, since more variables give more room/flexbility. One can try to make this notion mathematically precise, but the obvious precise versions of this would incorrectly predict that the Cassels-Guy cubic does have nonzero solutions.

 

In 1900, the David Hilbert listed 23 problems that he thought should be of the most importance for mathematicians to try to resolve in the 20th century. One of those problems, the 10th problem, was to find an algorithm which given a Diophantine equation tells you whether or not it has solutions. In the 1950s, Martin Davis and Julia Robinson almost showed that there was no such algorithm. They proved that there was no such general procedure if one allowed a slightly larger set of equations than what is normally called a Diophantine equation. In particular, note that in all of our examples, we've never had a variable in an exponent. For example, we haven't looked at something like 2^y = x^t + x^2 + x. Robinson and Davis proved that if one is allowed to have such equations (sometimes called "exponential Diophantine equations") that there was no algorithm to tell whether such an equation had solutions.

 

A few years later, Yuri Matiyasevich, building on their work showed that even for regular Diophantine equations, there was no solution to Hilbert's tenth problem. An important role was shown by essentially showing that one can make a Diophantine equation whose solution set in a certain sense looks exactly like the Fibonacci numbers. One consequence of Matiyasevic's work  was that even if one insisted that no variable be raised to a power higher than the fourth power, there was still no such algorithm. One obvious question then arises is whether the same thing is true for equations where there's no variable raised to a power greater than 3. No one knows. The Cassels-Guy cubic shows that if an algorithm does exist to solve such equations, it must have some substantial subtlety behind it.

An Introduction to Integer Complexity

(Note: I'm in the process of copying some older math posts from Facebook over here with some slight modifications. This is one of those.)

There are a lot of times people talk about famous open mathematical problems. But less attention is paid to some of the problems that are both simple to state and aren't very famous at all. Let's talk about one of those not so famous but still simple open problems.

We're interested in the minimum number of 1s needed to write a positive integer n as a product or sum of 1s, using any number of parentheses, and we'll call that ||n||. For example, the equation 6=(1+1)(1+1+1) shows that ||6|| is at most 5, since it took 5 1s. A little playing around will convince you that you cannot write 6 using just four or fewer 1s, so it is really is the case that ||6||=5. We call ||n|| the integer complexity of n.

Now here's the problem: Does every power of 2 have a most efficient representation the obvious way? That is, is it is always true f(2^k)= 2k? For example, 8=(1+1)(1+1)(1+1) and in fact ||8||=6. Similarly, 16 = (1+1)(1+1)(1+1)(1+1), and ||16||=8. (Note that we sometimes have representations which are tied for writing it this way; for example we can also write 8 = (1+1+1+1)(1+1) but that also takes 6 ones, not fewer).

One might think that the answer should be obviously yes, so let's look for a moment at powers of 5. Does every power of 5 have the obvious representation as best? We'd expect from ||5||=5, to get that ||25||=10, and we do. The pattern continues with ||5^3||=15, and ||5^4||=20, and ||5^5||=25, but then it breaks down, ||5^6||=29. This in some sense happens because 5^6-1 has a lot of small prime factors. But it isn't obvious that something similar couldn't happen with powers of 2. This problem was as far as I'm aware, first proposed by Richard Guy. This is a problem which is dear to me and one which I'm responsible for some of the progress on with Harry Altman who has written a lot about this problem on his Dreamwidth discussing his published works on the problem. 
 

My intuition on this problem keeps jumping back and forth on whether it is true or not. Right now, I'm leaning towards it being false.

Lehmer's Conjecture and Carmichael's Conjecture

(Note: I'm in the process of copying some older math posts from Facebook over here. This is one of those posts.) 

I've mentioned before that there are a lot of simple to state but not so incredibly famous open problems. I want to talk about two thematically related problems, Lehmer's Totient Problem, and Carmichael's Conjecture. These problems are well known to number theorists but don't have the same general fame as say Goldbach's Conjecture or the existence of odd perfect numbers.

Recall two numbers are relatively prime when their greatest common divisor is 1. For example, 15 and 8 are relatively prime. But 21 and 15 are not relatively prime because their GCD is 3. We'll define phi(n) to be the number of positive integers which are less than or equal to n and relatively prime to n. This function is known as the Euler phi function. For example, phi(9) =6 because under 9 we have 1,2,4,5,7 and 8 as numbers which are relatively prime to 9. Note that if p is a prime, then phi(p)=p-1. For example, phi(5) =4 since the numbers which are less than or equal to 5 and relatively prime to 5 are everybody: 1,2,3 and 4. (If you haven't seen the phi function before, it might be worth playing around with. Can you find phi(20)? What is phi of a power of 2? What is phi of a prime power in general?)

For a given positive integer a and another integer n we want to understand how big the smallest positive integer k is so that a^k leaves a remainder of 1 when we divide by n. For example, if a =2 and n =5, then one may take k=4, since 2^4 = 16 which leaves a remainder of 1 when we divide by 5. Similarly, if a=4 and n=7, then k = 3, since 4^3 = 64 which leaves a remainder of 1 when divided by 7.

Such a k doesn't always exist for a given n. If a and n share a common factor greater than 1, then so will a^k and n, and so the remainder of a^k when divided by n will also share the common factor, and so the remainder cannot be 1. For example, let's look at powers of 2 and their remainder when we divide by 10. We have 2,4, 8, 16, 32,64, 128, 256. When we divide by 10, we get as remainders 2,4,8, 6, 2,4,8, 6 ... And it keeps repeating this way.

But maybe there always is such a k as long as a and n are relatively prime. This turns out to be the case.

The first step towards proving this was due to Fermat. He proved what is now often called "Fermat's Little Theorem" (to contrast it with "Fermat's Last Theorem" but confusingly also abbreviated as FLT) which was that if p is prime, and a is not divisible by p (hence they must be relatively prime) then a^(p-1) leaves a remainder of 1 when one divides by p. So when n=p, we can in this situation always take p-1. The number p-1 may remind you of something, which we had earlier. When p was prime we had phi(p)=p-1. (A good exercise is to verify this works with p=7. That is, check that a^6 always leaves a remainder o 1 when you divide by 7 for a=1,2,3,4,5 or 6.)

And this is in fact the proper generalization! Euler proved a much stronger result: Recall we defined phi(n) be the number of positive integers which are less than or equal to n, and which share no common factor greater than 1 with n. Then Euler proved that if a and n share no common factor, then aphi(n) leaves a remainder of 1 when I divide by n. So, for k we care about is always at most phi(n). One might be interested in given an a and n what is the least value of k, and that's a delicate question that my own PhD work touched on. But that's a separate question. Phi(n) also shows up in some practical cryptographic applications, but that's not our emphasis today.

D. H. Lehmer in the 1930s was interested in how if p is a prime, then phi(p)=p-1. Lehmer noted that if n is composite then obviously phi(n) has to be strictly smaller than n-1, but maybe it fits in neatly to n-1. That is, maybe there is a composite number where phi(n) divides n-1? Lehmer conjectured that this was not the case. We don't know, but we do know that if there is such a number it needs to be pretty big (greater than 10^22 ), and it needs to have at least 15 distinct prime factors. If someone has the time and effort with some decent amount of computing power, they could likely improve this substantially. The technique used to obtain that bound is a little more clever than just checking every number under 10^22, but it doesn't involve deeply subtle number theory. My suspicion is that someone who is a good algorithmist and with some access to decent computing power should be able to improve that bound.

The other conjecture worth talking about in this context is Carmichael's Conjecture. Carmichael noticed that some numbers never arise as the value of phi(n). For example, phi(n) is always even if n >2. To see this note that if b is relatively prime to n, then so n-b, so after 2, numbers relatively prime to n and less than n always come in pairs. So any odd number other than 1 is never the value of the phi function. With a bit more work one can show that some other numbers don't arise either. For example, phi(x)=14 has no solutions.

But, Carmichael noticed that when there was a solution to phi(x)=k, there always seemed to be another y such that x was not equal to y and phi(y)=k. For example, we saw earlier that phi(5)=4. But phi(8) =4 also, since 1, 3,5 and 7 are the numbers which are less than or equal to 8 and relatively prime to 8. Carmichael conjectured that this was always true. That is, if phi(x)=k had a solution, then there was always more than one solution. Another similar example is how we saw that phi(9)=6, but it is also the case that phi(7)=6. (A good exercise: There are two other m such that phi(m)=6. Can you find them?). In this case, we also have very large bounds. In particular, we know that any counterexample to Carmichael's conjecture must be greater than 10^(10^10). That's pretty big.

How does one prove things about Lehmer's Conjecture?

Note: I'm in the process of copying some older math posts from Facebook over here. with some modification This is one of those.

I mentioned Lehmer's Conjecture  in an earlier post. Recently, someone asked me how one goes about proving something like the sort of result that a couunterexample needs to have a lot of distinct prime factors. I wrote an answer to them, and this is a version of that answer which may be of interest to people who read the earlier post. This post is slightly more technical than most of the other math posts currently here.

The primary technique used is the following. In what follows, I'll write capital N for a counterexample to Lehmer's conjecture, and use n for a generic integer where we aren't necessarily making that assumption. I'll implicitly assume that you've seen the Euler phi function a bit before. If not, the Wikipedia article is a good place to start . But the main takeaway we need about it is that if I have n=p^a for some prime p, then I can write phi(n) = (p-1)p^(a-1), I can multiply together the phi values at each highest prime power which divide n. For example, if n = 360, 180 =2^3 * 3^2 * 5 I can write phi(360)= phi(2^3) phi(3^2) phi(5) = (2-1)2^2 * (3-1)3^1 * (5-1) = 4*2*3*4=96. This formula will come in handy below. We won't need any other properties beyond what was mentioned in the previous post about Lehmer's Conjecture.

In the below, we'll write a|b to mean that a is a divisor of b. For example, 3|6 is true but 4|6 is false.  We'll need two preliminary remarks:

First, note that any such N must be odd. To see this, note that since phi(n) is even for n>2, if N is a counterexample, then N must be odd, since if N were even, N-1 would not be divisible by phi(N).

Second, note that any such N must be squarefree (that is not divisible by the square of a prime). To see this, note that from the standard formula for phi(n), if p^2 |n, then p|phi(n).

So if N is divisible by p^2 for some prime p, then since p|phi(n), we'll have p|N-1 and p|N which is impossible.

We'll define H(n) as the product of p/(p-1) over all primes which divide n. For example, H(60)= (2/1)(3/2)(5/4) = 15/4.

Important things to note about H(n). First, H(n) is multiplicative; that H(ab)= H(a)H(b) whenever a and b have greatest common divisor 1. Second, since x/(x-1) is a decreasing function, so if we replace a prime in the factorization of n with a larger prime, the value of H goes down. For example, H(3) > H(5) and H(20) > H(45).

Notice that H(n) = n/phi(n). Now, if phi(N)|N-1 for some composite N, then k phi(N) = n-1 for some k >1, and therefore we have H(n) = n/phi(n) > (n-1)/phi(n) = k. In particular, for any such N one must have H(N) > 2.

From this one immediately has that any such N has to have at least three distinct prime factors. To see this, note that H(15) = (3/2)(5/4) = 15/8 < 2, and again replacing any prime with a larger prime would result in H being even smaller.

To give a flavor of the general method, let's sketch a proof that N needs to have at least five distinct prime factors.

One Lemma that will be helpful first:

Lemma 1: If N is a counterexample to Lehmer's conjecture and p|N for some prime p, and q|N for some prime q then we cannot have p|q-1.

Proof: Assume we had such, then by the formula for phi(n) we'd have p-1|N-1 and hence q|N-1 since q|p-1. But we cannot q|N and q|n-1.

(For example, this Lemma shows that we cannot have both 3|N and 7|N. Very handy little bit.)

Theorem: There is no such N with three distinct prime factors.

Proof: Assume that N is such an N. Note that (5/4)(7/6)(11/10) < 2. So our smallest prime factor must be 3. So 7 does not divide N by our Lemma. Similarly, since (3/2)(11/10)(13/12)< 2, our second largest prime factor must be 5, and thus by our Lemma our third prime factor cannot be 11. It also cannot be 13 by our Lemma. We now need a prime p (3/2)(5/4)(p/(p-1) > 2. But solving this inequality one will find that one needs p<17, so there are no primes which remain to check.

Now we'll sketch the same technique for the slightly harder case of four distinct prime factors. But the above shows most of the central ideas. Below will be essentially just an elaboration of the same technique.

Theorem: No such N has four distinct prime factors.

Proof:We'll break this down into two cases, based on whether 3 is a prime factor of N.

Case I:Assume 3|N. By our Lemma, we cannot have 7, 13 or 19 as divisors of N. Now, we'll break this down into two subcases based on whether 5|N.

Case Ia: 5|N. In that case, by our Lemma we have that 11 does not divide N. Let's break this down slightly further. Note that if the second largest prime factor of N is 29 then since (3/2)(5/4)(29/28)(47/46)< 2 we have a contradiction. (Exercise: Why was I able to get away with skipping 31, 37, 40 and 43 as possible prime divisors?). So we have some subcases where the third prime factor is 17, 23 or 29. If the third prime factor is 17, then we must have for the fourth prime factor p, that (3/2)(5/4)(17/16)(p/(p-1)) > 2. Solving for this, one will find that one must have p <= 257. Now, checking all primes which are at most 257 will find that none of them work. Similarly, one can do the same thing if the third prime is 23 or 29. (If one is lazy and is doing this with a computer one doesn't even need to calculate the precise largest bound for when (3/2)(5/4)(23/22)(p/(p-1)) > 2, since we know it must be no higher than 257. The same remark applies to 29.)

Case Ib, where 5 is not a divisor of N. Then we have (3/2)(11/10)(17/16)(23/22) < 2 so we're done. (Note that if this hadn't been less than 2 we could have used that we can't actually have both 11|N and 23|N so we could have broken this down further but we didn't need to).

Case II: We've assumed that 3 doesn't divide N. Note that (5/4)(7/6)(11/10)(13/12) < 2, so we're done. (Again note that if this had been too large we could have broken down into subcases depending on whether 5 divides N and then thrown 11 out in one of them.)

That's the basic technique. In practice, one wants to do as much of this as one can via computers and there are a few other ideas and tweaks which one can do to save on case checking.

Richard Guy, 103

Richard Guy passed away yesterday morning, on March 9th. Guy was a mathematician at the University of Calgary. He was 103 years old and had been steadily working right up until his death.

 

I've interacted with him in a bunch of different contexts, and his "Unsolved Problems in Number Theory" was a major influence on my work and a lot of what I do. Almost every paper I've written was influenced by his wonderfully comprehensive collection of problems. Although I had corresponded with him via email, it wasn't until a few years ago at the JMM that I met him in person, where he struck me as a kind and thoughtful person, very interested in what others were doing. He was a great influence on me and many other young mathematicians.

 

In a certain sense almost everyone dies too young, but it feels strange to say that about someone at 103. But in Richard's case, I'm willing to say it. We had more to learn from him, and he had more to teach and discover. It is a cliche to say that someone will be missed, but in this case, it is true. He will be missed by many mathematicians all over the world, in many different fields. I feel sorry for the now young mathematicians who will get to read his books but not get to actually meet him.

Differential Equations, SIR models, and COVID-19

A lot of people have wondered why there's so much concern about COVID-19. I've taught classes on both differential equations and graph theory before with some degree of disease modeling, so I have some relevant expertise, although certainly much less than a trained epidemiologist or someone whose research focuses on disease modeling. In that context, I want to discuss some of the reasons why this is generating more concern than the regular flu from a mathematical standpoint.

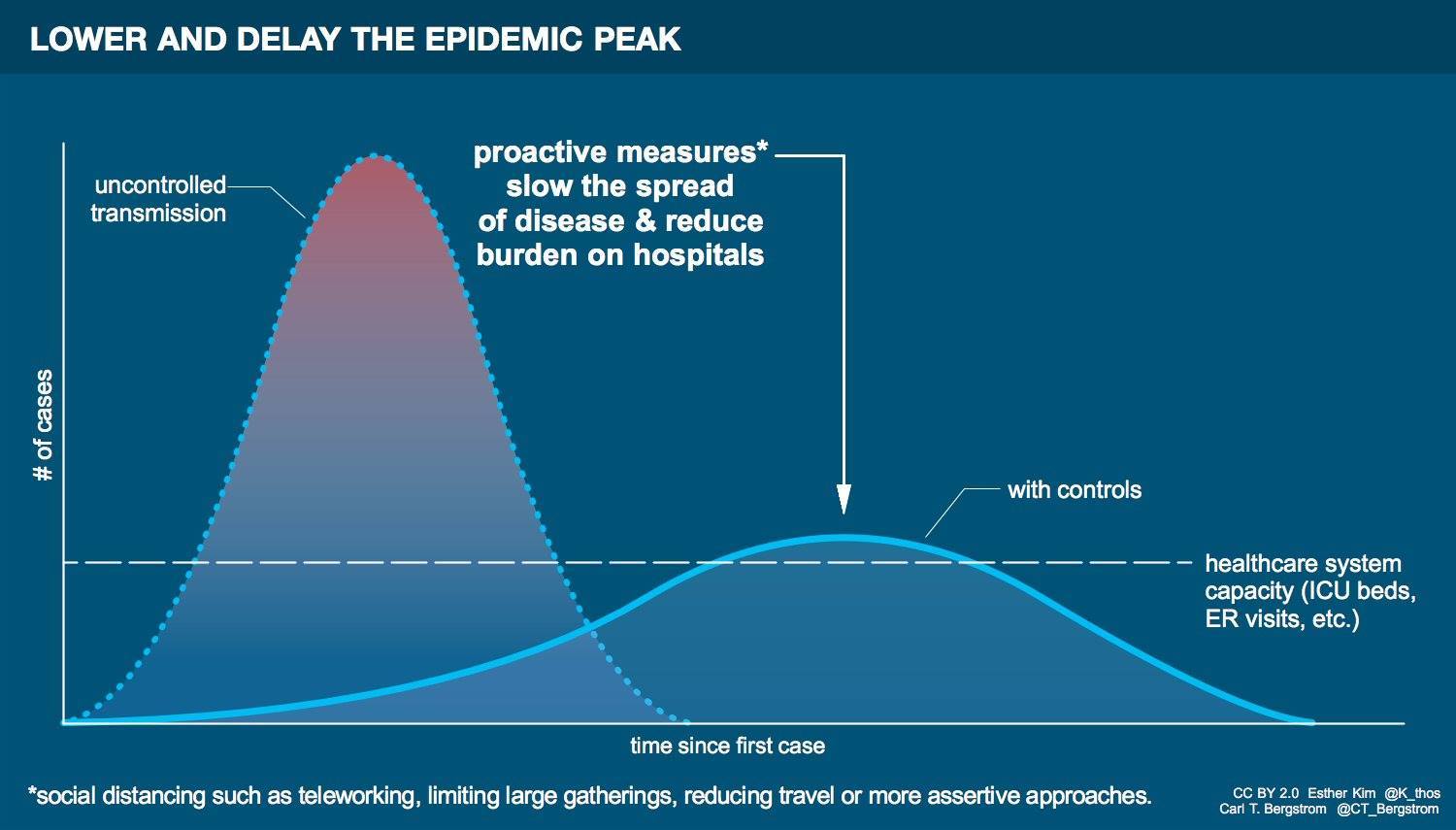
The most common basic model of disease spread is the SIR model , and it turns out that simple versions of this model work pretty well empirically for many diseases. The basic idea of the model is that one has three compartments representing three types of people, people who are susceptible to the disease but are uninfected, people who are infected, and people who have recovered. People move from the susceptible to the infected category based on the number of people infected, with some parameter representing how likely an infected person is to infect new people. People move from the infected to the recovered population at some fixed probability. Strictly speaking "recovered" for our purposes also includes people who died and thus aren't spreading the disease but that distinction doesn't matter much for this sort of model. The basic model assumes that once one is in the recovered category one is either dead or immune.

When one uses this sort of model, and one looks at the disease presence over time the basic pattern one gets is a large hump followed by the number of infected then trailing downwards. For a graph of this sort of hump occurring in China with this virus, along with a lot of other good data, see here.

This is the basic model, and one can do a lot of things to play with the model. For example, one can imagine one has a vaccine for some people; this moves some people directly from the susceptible box into the recovered box. This drastically reduces the size of one's hump. Another thing one can do is have more than three boxes; one can imagine each region (say a city, school or nation) with its own set of boxes but then a chance for people infected in a region to infect people in a nearby region. One can also imagine diseases which have long periods of spread and infection, so the presence of births in the population become relevant. A good exercise is to think of some other thing you'd want to add to this sort of model.

As these models get more complicated, much of the modeling becomes empirical, running many different small variants of a model with computer approximations rather than much emphasis on analytic techniques; there's not as much as we can satisfactorily prove about some of these models as we'd like from a mathematician's perspective.

In this context, let's talk about three things which make from an SIR perspective this virus to be potentially worse than influenza (aside from the higher mortality rate which while also concerning isn't something that the SIR perspective really models much):

First, not everyone who gets the virus becomes immune after they recover; we're seeing not just relapses but evidence of reinfection. One essentially has some people who would move from infected to recovered but instead are moving back to susceptible. If one plays around with SIR models one will see that having such movement can easily make epidemics much worse. We're not completely certain that such reinfection is occurring but it looks likely. One difficulty is trying to distinguish reinfection from relapse. There's some evidence for low-level infections in people who are otherwise considered to have recovered. Trying to figure this out is going to be something doctors are thinking about very carefully. This is a general news article discussing some of the issues involved.

Second, the contagion rate of this virus appears to be higher than that for influenza. While there's a lot of uncertainty about the reproduction rate, R_0, which roughly speaking, represents the number of average new infections from infected individual, those numbers range from about 2.2 to about 4.5 and they seem to be likely on the higher end. In contrasts, many estimates for influenza put this number for it at at most 2; for the 1918 flu the number was probably between 2 and 3. Increasing R_0 has for what should be obvious reasons, a pretty severe impact on the severity of epidemics. The exact translation of R_0 into the SIR has some subtleties, and estimates for R_0 do change for diseases. They frequently start off larger than they would be otherwise until procedures targeting a disease are in place. There's some substantial criticism of R_0 as a metric in general , but as a rough guide it is useful here. There's also been some statement by the WHO (such as here) saying that at least by some metrics, COVID-19 is less efficient at transmission than the flu. I''m not sure what metrics they are using there, but if that's accurate that's a major reason to be less worried.

Third, there are people who get infected and are contagious but are almost completely asymptomatic. That basically doesn't happen with flu almost at all, and that means that containment is much harder. (This is not double counting evidence with the R_0 point above because those estimates are generally for people who do exhibit symptoms.) We're still uncertain how often this happens. In the case of influenza, people can be infectious before any substantial symptoms appear, but symptoms always show up. In the case of this virus, there appear to be some people, especially young people, who are not just infectious while being asymptomatic, but remain completely asymptomatic. Even a tiny percentage here can drastically interfere with containment efforts.  Remember how I mentioned how one variant of SIR models involves triplets of boxes each for a different location? Well, if you do that, you can model how effective travel restrictions and quarantines are, and they become substantially less helpful if there are completely asymptomatic people. It only takes one infected person to enter a new location.

Right now one of the biggest issues is simply how many unknowns there are. It could turn out that all three of these issues above aren't that severe. Or it could turn out that all three are substantially in play. We don't completely know at this point, and have a worrying amount of evidence that all three of these issues are cropping up.

In this context, one might wonder why taking steps to delay infection matter. In these models, people get infected and eventually move over to recovered, so you might think that everyone gets infected. But that's not actually the case. Eventually, a disease becomes low enough levels that some people who are in the susceptible box category never get infected. If one can delay infection the number of people left in that box at the end stages can get bigger. Another major issue is the maximum number of infected. Remember the hump I mentioned above? The size of that hump matters a lot from a treatment perspective because ill people aren't as economically productive and many of them will need to be in hospitals, taking up limited hospital bed space. Even if the total number of infected were to remain the same over the entire period, the stress on the hospital system will be lower, resulting in likely fewer deaths from the disease, or deaths from other medical issues as the entire system is subject to less of a resource crunch. There's also the issue that other treatments may be developed; the longer we delay things the higher the chances that more people will be saved by new treatments.

In this context, what can you do? Washing hands and not shaking hands are steps which have been mentioned by many but I'll repeat them here; they can't be emphasized enough. But aside from that, buying extra non-perishable goods that are frequently used is the obvious place to start. One doesn't need at this point to run out and buy all the toilet paper (looking at you Australia), but having a few extra days of food, and yes toiletries, is not a bad step. When you go to the store, buy a few extra food items. You don't need to buy them all now, but but buy a few, and then put them away, and (this bit is a important) don't count them as present when calculating whether you need to pick up more food in the future, until the disease is passed. The same goes for some other basic items, medicines and the like when possible and practical.

Another thingy you can do is get the flu vaccine. While Trump's comments about the flu vaccine for COVID-19 were, not surprisingly, stupid and ignorant, there are two good reasons to get the flu vaccine if you have not before. First, for many diseases, multiple infections are a major cause of fatalities. With the 1918 flu, many who died died not directly from influenza but from bacterial infections which occurred with it and this is a pretty standard pattern for deaths from influenza or similar illnesses. Second, the flu vaccine makes it less likely that one will need to be hospitalized for flu; that's even more important now than it usually is, because of the possible issues with limited hospital resources. If we can minimize stressing the system as a whole, we'll be in better shape.